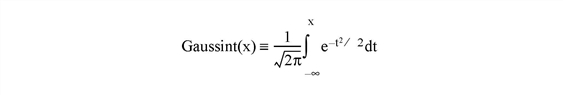
The GAUSSINT function evaluates the integral of the Gaussian probability function.
The Gaussian integral is defined as:
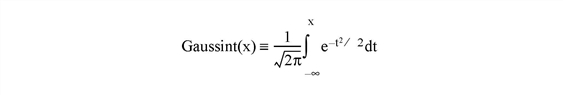
Result = GAUSSINT(X)
Returns the result of the Gaussian probability function integral evaluation. If X is double-precision, the result is double-precision, otherwise the argument is converted to floating-point and the result is floating-point. The result has the same structure as the input argument, X.
The expression for which the Gaussian integral is to be evaluated.
This routine is written to make use of IDL’s thread pool, which can increase execution speed on systems with multiple CPUs. The values stored in the !CPU system variable control whether IDL uses the thread pool for a given computation. In addition, you can use the thread pool keywords TPOOL_MAX_ELTS, TPOOL_MIN_ELTS, and TPOOL_NOTHREAD to override the defaults established by !CPU for a single invocation of this routine. See Thread Pool Keywords for details.
Plot the Gaussian probability function over the range -5 to 5 with a step size of 0.1by entering:
X = FINDGEN(101)/10. - 5.
PLOT, X, GAUSSINT(X)
|
Original |
Introduced |